Pendule de Foucault: Théorie rapide

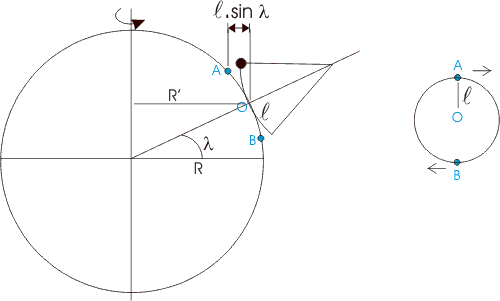
                Plaçons nous à une latitude l. Le schéma de gauche montre la Terre de côté, le pendule est lâché initialement sur une direction Nord-Sud. Le schéma de droite montre le pendule vu d'au-dessus de sa position d'équilibre. Les points A, O et B sont des points de la surface terrestre, séparés par la distance l, qui correspond à l'écart maximum du pendule au sol.

                Quand la masse est en équilibre en O, elle se déplace autour de l'axe de rotation terrestre à la vitesse: v_O = R'.w (où w est la vitesse angulaire de rotation de la Terre sur son axe / étoiles)

                O a une vitesse plus grande que A, elle est augmentée de l.sin l.w car O est plus loin de l'axe que A. Donc, quand la masse arrive en A, elle possède une vitesse "vers la droite" plus grande que A de cette valeur.

                O a une vitesse plus petite que B, elle est diminuée de l.sin l.w car O est plus près de l'axe que B. Donc, quand la masse arrive en B, elle possède une vitesse "vers la gauche" par rapport à B, qui a cette valeur.

                Ceci implique que par rapport au sol, dans l'hémisphère Nord, le plan d'oscillation tourne dans le sens des aiguilles d'une montre, et comme

                l.sin l.w = l.W ou W est la vitesse angulaire de rotation de ce plan, on a: sin l.w = W

                Ou encore, en passant aux périodes: sin l / 24 = 1 / T où T est la période en heures.

Et enfin: