Le point situé à
l'horizon est marqué par la ligne de visée tangentant la
surface terrestre.
A quelle distance se trouve l'horizon?
Supposons nous à la plage, le temps est clair et dégagé. Des navires croisent à l'horizon. S'ils s'éloignent davantage, ils sembleront s'enfoncer derrière cette fameuse ligne d'horizon: c'est probablement ce qui faisait craindre aux anciens marins de passer par dessus le rebord du monde. Cela a été, et reste un très bon argument indiquant que la Terre est ronde. Si elle était plate, l'horizon serait à l'infini, et un navire s'éloignant deviendrait de plus en plus petit, mais sans disparaître sauf si les brumes sont trop denses...
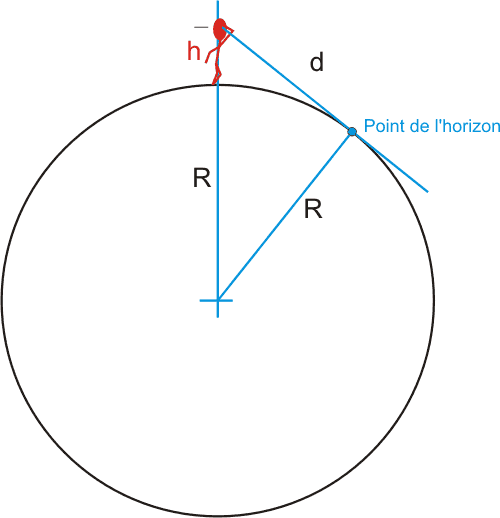
Voyez un schéma explicatif, qui a une petite chance d'éclairer les choses:
|
|
Le point situé à
l'horizon est marqué par la ligne de visée tangentant la
surface terrestre. |
| Ce croquis contient la réponse à la question: un grand coup de ce bon vieux théorème de Pythagore indique: |
| R² + d² = (R + h)², qui se simplifie un peu, à supposer que le rayon de la planète soit bien plus grand que votre taille (ce qui arrive assez souvent finalement), en d² = 2.h.R |
Ainsi, si vos yeux sont à 1,55m au-dessus de la plage (h), et que le rayon de la Terre est de 6400km (R), on trouve que l'horizon est à 4500m (d).
Bien sûr, plus vous serez haut, et plus vous pourrez voir loin: c'est la raison pour laquelle les phares maritimes sont construits en hauteur.
Pour finir, observez la forme ronde de la Terre depuis la plage: ce navire est derrière l'horizon, sur les images suivantes.
Il est loin de nous sur l'image de droite et plus proche à gauche. On n'en voit que les parties supérieures dans les deux cas, mais quand même un peu plus sur l'image de gauche. Alors, elle n'est pas ronde cette planète?...
