Mesurez le rayon de l'orbite de Vénus, à partir des observations de Galilée:

Voilà une intéressante petite activité, aussi bien astronomique qu'historique. Les données de départ sont fournies par un illustre expérimentateur, Galilée lui-même, qui a fait ses observations avec une lunette d'une qualité plus que discutable il y a 4 siècles. Cependant, rien ne vous interdit de faire vous même quelques images de Vénus. Deux suffisent: une quand elle est proche de nous (conjonction inférieur), l'autre lorsqu'elle est au plus loin (conjonction supérieure). L'inconvénient est que dans les deux cas, Vénus est très proche angulairement du Soleil, l'observation n'en est donc pas très aisée, dans les lueurs crépusculaires, mais ça vaut la peine d'être tenté, même de jour si vous le sentez!...

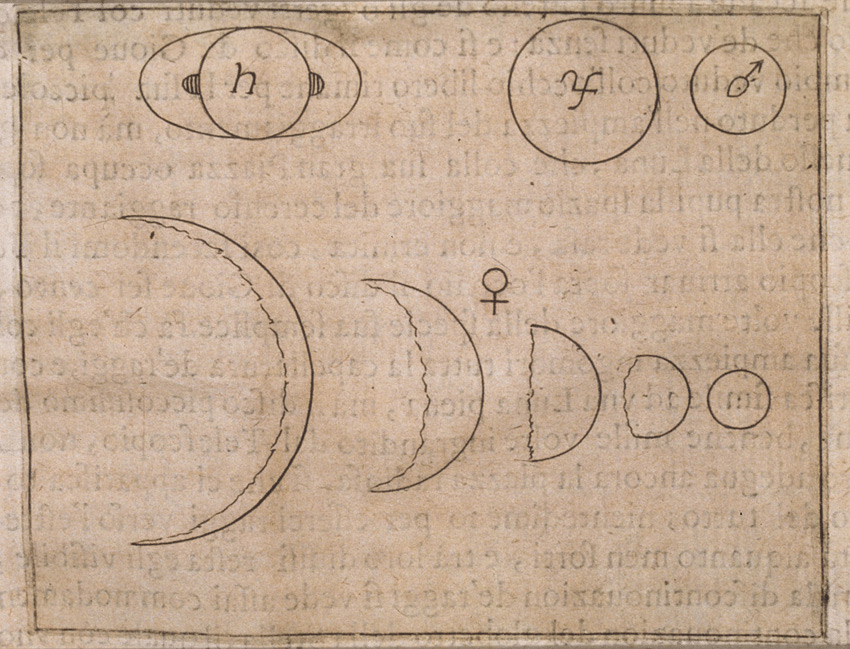
Galilée a donc dessiné ceci:

En haut à gauche, vous reconnaîtrez peut-être Saturne et ses anneaux, puis Jupiter, et Mars. Cinq phases successives de Vénus sont représentées en dessous.

Donc, deux observations fondatrices: le diamètre apparent de Vénus change fortement, et elle présente des phases. Il y a une donc deux conséquence cruciales:

--Si le diamètre apparent change, c'est que la trajectoire de Vénus ne peut pas être un cercle centré sur la Terre. On élimine donc le système géocentrique, sinon, le diamètre apparent de Vénus resterait constant, sa distance à la Terre ne variant pas.

--Si la phase de Vénus change, c'est que l'orbite de Vénus, autour du Soleil, est interne à celle de la Terre. En effet, une planète externe, comme Jupiter semble forcément toujours éclairée sensiblement de face, vue de la Terre.

On peut alors en déduire le plan du système Terre-Vénus-Soleil: c'est celui-ci:

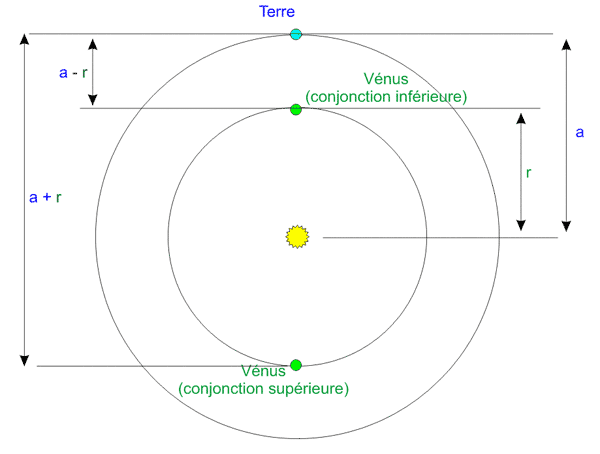
Quelques petites approximations: les orbites sont des cercles, et on suppose que quand Galilée dessinait Vénus avec le plus grand diamètre, elle était proche de la conjonction inférieure, et du côté de la conjonction supérieure pour le petit diamètre apparent.

Le rapport des diamètres apparents est identique au rapport des distances, mais à l'envers (si la distance est faible, le diamètre apparent est grand)

Ce qui se traduit par:

Puisque 5,7 est le rapport des deux diamètres apparents, mesuré sur le dessin de Galilée.

Comme vous êtes des dieux en algèbre, vous en déduisez que:

a + r = 5,7 x ( a - r )

donc 6,7 x r = 4,7 x a

Et enfin r = 0,7 x a

Comme "a", le rayon de l'orbite terrestre vaut 1 u.a (unité astronomique), c'est que le rayon de l'orbite Vénusienne vaut 0,7 u.a

Et notre ami Wikipédia nous annonce 0,72 u.a

Pas si mal finalement, pour des mesures faites il y a plus de 400 ans, avec un matériel douteux... Vous pourriez faire mieux? Peut-être, c'est à voir...