
A gauche Jupiter, et l'ombre de Ganymède situé à droite. Encore plus à droite, Europe. 25 janvier 2012, 19h20TU. Télescope 200/800mm, tirage oculaire
Comment utiliser une éclipse sur Jupiter pour reconstituer un plan du système jupiterien?
A partir d'une image unique, la mission est cette fois de retrouver la position d'un satellite de Jupiter en vue de dessus. Il ne faut pas n'importe quelle image, mais une sur laquelle on a le plaisir de découvrir l'ombre du satellite, une éclipse jupitérienne en fait. Voici un exemple de document:
 |
A gauche Jupiter, et l'ombre de Ganymède situé à droite. Encore plus à droite, Europe. 25 janvier 2012, 19h20TU. Télescope 200/800mm, tirage oculaire |
Faisons déjà parler cette image: Elle a été prise après l'opposition (le moment où la Terre doublait Jupiter, quand le rapprochement des deux planètes était minimum). Cela se voit ici, car si on était à l'opposition, on aurait Jupiter éclairé parfaitement de face, or on voit que le bord droit est plus net que le gauche, donc, l'éclairage provient légèrement de la droite. On soupçonne alors qu'il est normal que Ganymède projette son ombre sur l'atmosphère de Jupiter, alors qu'il est fort décalé à droite. Cela donne ce genre de disposition:
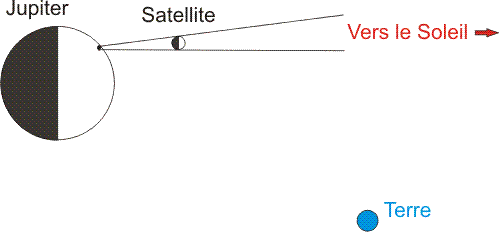
Le but du jeu va être de reconstituer en vue de dessus, les positions relatives de Jupiter et de son satellite, voire même de retrouver le rapport du rayon de l'orbite du satellite sur le rayon de Jupiter. Voici les croquis de base de la réflexion:
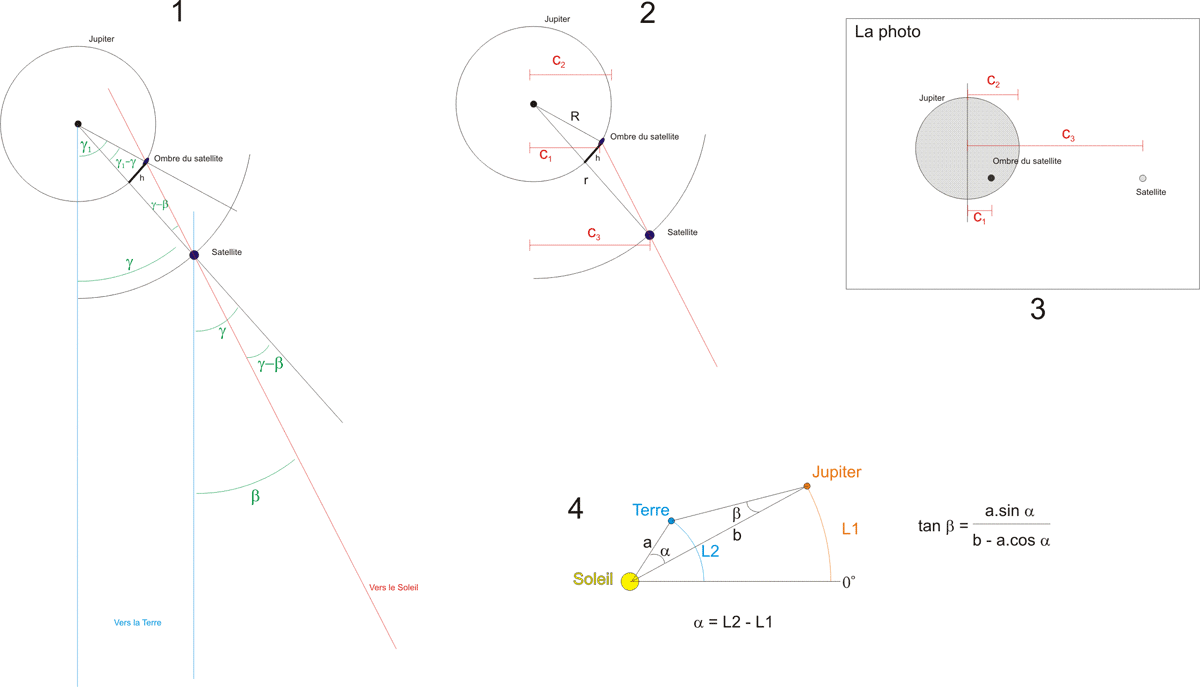
Ne partez pas tout de suite! Oui, je sais, ça fait un peu peur, mais on a vu pire...
1/ Les mesures sont faites sur la photo (C1, C2 et C3, en pixels, respectivement la distance à l'axe de l'ombre du satellite, le rayon de Jupiter et enfin la distance du satellite) (figure 3 du document)
2/ On a besoin de l'angle "Béta", vu depuis Jupiter entre les directions de la Terre et du Soleil. Pour cela, le logiciel "Heliocentrique" vous aidera: il donne les longitudes des 2 planètes (L1 et L2), qui permettent de trouver "béta", voir figure 4 du document.
3/ La figure 1 donne les liens entre tous les angles tordus existants dans la situation. Avec un peu de patience, vous trouverez:
4/ Trouver "gamma", c'est trouver l'angle réel de position de Ganymède autour de Jupiter. r/R sera trouvé grâce à l'équation 5. Mais comment trouver "gamma"? En résolvant la dernière équation? Non, vraiment, merci... Heureusement un tableur nous sauvera: il suffit de lui demander de calculer une liste de valeur du terme 1 en incrémentant "gamma", de faire pareil avec le terme 2, quand les deux sont égaux, c'est qu'on a le bon "gamma"!...
Voici des mesures approximatives faites avec l'image présentée en début d'article:
| c1: 7 pixels |
| c2: 62 pixels |
| c3: 202 pixels |
| L1 - L2 = alpha: 81° |
| Donc béta calculé: 11° (à partir de a = 1ua et b = 5,2ua |
Tout ça mis dans un tableur donne:
Les deux termes deviennent égaux pour "gamma" valant aux environs de 11°, ce qui donne un "r/R" aux alentours de 17 (15 d'après les valeurs moyennes trouvées sur le net). Ce qui donne en final, la représentation à l'échelle (sauf pour la taille de Ganymède):
Tout ça pour ça... Je suis d'accord, mais quand même... On l'a fait avec nos petites mains...