Comment mesurer la distance Terre-Lune?
Là, on va toucher à l'exploit
historique: après avoir sondé les profondeurs du monde
submicroscopique, attaquons nous au
monde des distances astronomiques!
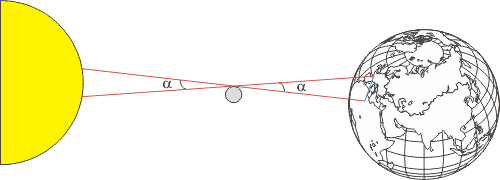
La méthode est basée sur le
principe des parallaxes: deux observateurs distants sur Terre, ne voient pas la
Lune se projeter sur le même fond de ciel. Il nous faut donc deux observateurs
sur Terre (distants de quelques centaines de kilomètres), une Lune (ça doit se
trouver), et un fond de ciel reconnaissable, ce sera ici... le Soleil. La
situation est donc celle d'une éclipse, et le Soleil sera considéré comme étant
à l'infini (c'est une approximation, bien sûr, mais raisonnable dans ce cas, par
rapport à la distance Terre-Soleil: 400 fois plus grande que la distance
Terre-Lune).
Voici le schéma de principe:
| |
Les deux observateurs terrestres ne voient pas le
"sommet" de la Lune se projeter au même endroit à la surface du Soleil.
L'angle a sera d'autant plus grand que
la ligne de visée est longue, vue depuis la Lune. Si on connaît les
deux, on a la distance Terre-Lune... |
Lors de l'éclipse annulaire du 3
octobre 2005, nous étions dans le sud de l'Espagne, à Gandia pour en profiter.
Yves, un ami avait la "chance" de pouvoir l'observer en France près de Nice, où
elle n'était que partielle. Comme il n'est pas rancunier, il m'a confié une
image qu'il a prise du phénomène, à 09h (Temps universel), au moment de la
centralité en Espagne.
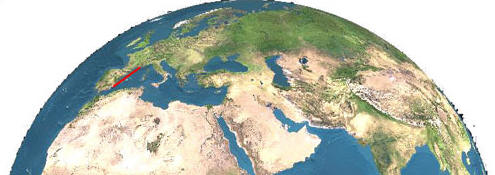
Voici les 2 images, prises au même
instant:
| |
| A gauche, Nice, à droite Gandia (près de Valencia).
La distance du bord lunaire au bord solaire n'est visiblement pas le même
depuis les deux sites d'observation. Ce qu'il faut mesurer est indiqué
ci-dessous: |
| |
| Pour l'image annulaire, vous verrez peut-être
qu'elle n'est pas tout à fait centrée. Je conseille de prendre la moyenne
des deux extrêmes trouvés. La différence entre les deux distances au bord
du Soleil trouvée correspond à l'angle a
du schéma précédent, avec pour référence le diamètre apparent du Soleil
qui valait 32 minutes d'arc ce jour là (32 fois 1/60ème de degré).
Si
vous cliquez ici, vous pourrez télécharger une image de plus grande
taille à imprimer pour faire les mesures. |
Les
mesures donnaient:
| Depuis Nice: Lune à 30 mm du bord |
| Depuis Gandia: Lune à 3,5 mm du bord |
|
D'où un écart de 26,5 mm |
| Et comme diamètre apparent du Soleil: 32 minutes
d'arc |
| Diamètre du Soleil sur le papier: 135 mm |
|
D'où, l'angle a =
32 x 26.5 /
135 = 6,28 minutes d'arc |
Mais il
nous faut maintenant la longueur de la ligne de base Nice-Gandia, telle qu'on la
voit depuis la Lune (ou bien projetée sur la droite perpendiculaire à l'axe
[bord de lune - milieu Nice-Gandia]). Cela pourrait être fort compliqué à
calculer, mais tout simple grâce à une petite astuce. Il existe un site (http://www.fourmilab.ch/earthview/vplanet.html)
qui donne une image de la Terre vue depuis la Lune aux dates et heures choisies.
| |
| Il suffit de mesurer sur le papier ou à l'écran la
distance entre les deux sites, et, connaissant le diamètre terrestre
(12756 km), obtenir la distance cherchée.
Si
vous cliquez ici, vous pourrez obtenir une image entière et plus
grande de la situation (100 ko). |
Là, les
mesures donnent:
| Distance (papier) Gandia-Nice: 12 mm |
| Diamètre de la Terre (papier): 203 mm |
| Diamètre réel de la Terre: 12756 km |
|
D'où, la distance mesurée entre Gandia et Nice:
= 12 x 12756
/ 203 = 754 km (vu de la Lune) |
|
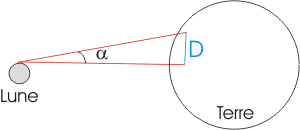
Voilà, c'est presque fini, il ne reste plus qu'à combiner nos deux mesures
(angle et longueur de la ligne de base) avec la célèbre formule de
trigonométrie: Distance
Terre-Lune = 754 / tan 6,28' = 412775 km (depuis la surface de la Terre) |
|
On ajoute le rayon terrestre pour avoir la distance de centre à centre, ce qui
donne environ 420000 km au lieu de 400000 km donné par les éphémérides (soit 5%
d'écart). Pas si mal non?
Bientôt, a nous les étoiles!!...