Comment mesurer la distance d'un astéroïde au Soleil en deux images?...

La méthode décrite ici est applicable aussi bien aux astéroïdes qu'aux planètes du système solaire. Mais bon, comme il y a de moins en moins de planètes dans notre système, et de plus en plus d'astéroïdes... Les calculs effectués supposent les orbites circulaires. On supposera également qu'elles sont à peu près dans le plan de l'écliptique... Le but étant d'obtenir un ordre de grandeur, et même un peu mieux, alors, ne chipotons pas!

Le principe n'est pas trop compliqué: les planètes tournent plus lentement autour du Soleil si elles en sont plus loin. Cette vitesse orbitale ne dépend que de la distance au Soleil (si l'orbite est circulaire, rappelez vous). Si on parle d'une planète ou d'un astéroïde externe à l'orbite terrestre, son mouvement apparent sur le fond de ciel est dû à une combinaison de la vitesse de la Terre et de celle de l'astéroïde. De même qu'en auto sur l'autoroute, si vous suivez une voiture, sur une autre file, vous la voyez progresser par rapport aux éléments lointains du paysage, et même reculer par rapport à ceux-ci quand vous la doublez, la Terre double les planètes lointaines sur son orbite: on les voit alors progresser à des allures différentes par rapport aux étoiles, suivant les positions respectives des protagonistes autour du Soleil.

Voici un exemple de données: Deux images de la position de l'astéroïde Vesta, à une journée d'intervalle.

L'autre information nécessaire, qui serait mesurable ausi d'ailleurs, mais n'en rajoutons pas, est l'élongation moyenne de l'astéroïde lors des prises de vue. Elle est trouvable grâce à des logiciels de cartographie du ciel gratuits, comme l'excellent "Carte du Ciel" de Patrick Chevalley. Par exemple ici, Vesta avait une élongation de 120°, c'est l'angle entre le Soleil et l'astéroïde, vu depuis la Terre.

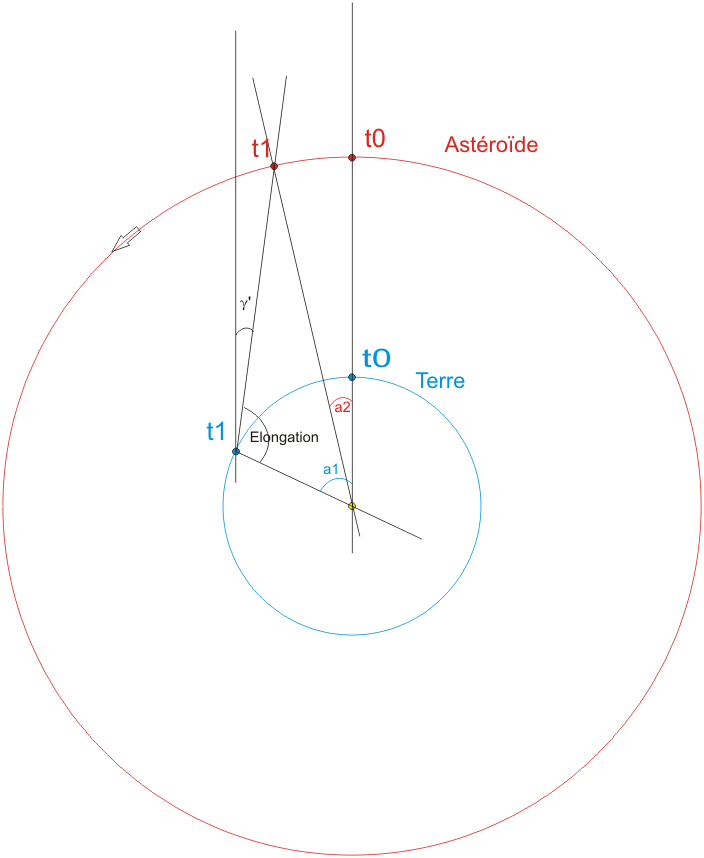
Entre les dates t0 et t1, Vesta et la Terre se sont déplacés, à leurs vitesses respectives. La Terre a tourné de l'angle a1, alors que Vesta n'a parcouru que a2. Le déplacement de Vesta sur le fond de ciel lointain et étoilé est matérialisé par l'angle gamma' du schéma.

Maintenant, en supposant tout connu de l'orbite terrestre (vitesse orbitale de 30 km/s et rayon de l'orbite de 150 millions de km ou 1 unité astronomique (ua)), il faut, à partir de l'élongation et du mouvement apparent de l'astéroïde, trouver sa distance au Soleil. On devine que plus l'objet est lointain et plus sa vitesse est faible, et qu'alors son déplacement apparent est plus fortement conditionné par le mouvement terrestre... Il doit bien y avoir une équation à résoudre qui relie tout ce petit monde... Sûrement...

Mais c'est trop compliqué pour moi...

Alors, demandons à un tableur de calculer les positions successives de la Terre et de Vesta (en imaginant une valeur fictive de sa distance au Soleil) en sachant simplement qu'à chaque distance correspond une vitesse orbitale circulaire. L'angle parcouru (a) est calculable par la formule ci-contre.

Comme le tableur affiche tous les angles successifs en foction du temps, des deux planètes, on peut lui demander de calculer aussi l'élongation et gamma' du schéma précédent. Et tant qu'on y est, lui suggérer poliment de nous fournir de déplacement apparent de Vesta vu depuis la Terre.

Bien sûr, la valeur de la distance de Vesta au Soleil introduite initialement ayant peu de chance d'être la bonne, pour l'élongation de 120°, il y n'y a guère d'espoir d'avoir le déplacement réellement mesuré (environ 2,5 minutes d'angle à partir des images). Mais il suffit de modifier la valeur de la distance de Vesta (en référence absolue dans une cellule du tableau) pour que par tâtonnements successifs, on ait la bonne correspondance "élongation-déplacement apparent"... Visuellement, ça fait un peu peur, mais ça donne cela:

La seule cellule à modifier par essais successifs est la cellule en vert (distance de Vesta en u.a.). Tout le tableau est alors recalculé. J'ai surligné en jaune la zone où l'élongation de Vesta (en rouge) est d'environ 120°, il faut alors que le déplacement apparent de l'astéroïde (en bleu) soit voisin de la mesure effectuée: 2,5 min d'angle. On l'obtient ici pour un choix de 2,6 unités astronomiques, alors que la valeur trouvée dans la "littérature" est d'environ 2,4 ua. Donc environ 8% d'écart.

J'oubliais... La feuille de tableur toute faite (adaptée à Excel) est ici...

Amusez-vous bien, avec vos astéroïdes à vous!...