Mesurer la distance d'un amas d'étoiles? Vraiment? Je peux?...

    Cette fois, c'est du côté des échelles astronomiques que nous partons. Nous allons tenter de comprendre comment mesurer la distance d'un amas d'étoiles, et en plus, le faire pour de vrai!...

Comment réaliser cet exploit? Il faut partir d'observations pas vraiment intuitives, mais relativement faciles à réaliser. Notre cible devra présenter quelques propriétés exploitables: ce doit être un amas plutôt jeune, pas trop éloigné (cela peut aller jusqu'à plusieurs centaines d'années-lumières tout de même), aux étoiles individuellement bien distinctes. Supposons que nos étoiles membres de l'amas aient environ toutes le même âge (ce qui n'est pas une supposition exagérée, ni forcément tout à fait nécessaire, vous le verrez plus loin). Supposons également qu'elles soient toutes à la même distance de nous (la taille de l'amas est en fait petite par rapport à son éloignement). Alors, les différence d'éclats des étoiles entre elles ne sont dûes qu'à leurs véritables différences de luminosités propres.

Notre cible sera l'amas des pléiades, très célèbre dans le monde des amateurs d'observations du ciel. Il est visible sans soucis à l'oeil nu, dans la constellation du Taureau. Il est aussi facilement photographiable ou "imageable". Je vous conseille un téléobjectif de 300mm si vous utilisez un appareil réflex argentique, un 200mm doit faire l'affaire en numérique.

Il ne sera pas utile de chercher à faire une très belle image, où les nébulosités ressortent bien et donne un aspect particulièrement esthétique à l'image. Par contre, vous tenterez d'en faire deux: l'une faite avec un filtre vert, et l'autre faite avec un filtre bleu. Pour vous guider, les filtres sont souvent repérés par leur code Kodac Wratten. Pour le vert, essayez le n:58, et pour le bleu, tentez le n:80A. Il vous faudra probablement faire quelques essais de temps de pose, les deux filtres n'étant pas du tout équilibrés (ils n'ont pas la même capacité de transmission).

Voici deux essais, pas brillants, réalisé avec une caméra Meade DSI pro montée derrière un téléobjectif de 210mm.

	Voici l'image faite avec le filtre bleu...(cliquez ici pour en obtenir une version plus grande)
	... Et celle obtenue avec un filtre vert. D'accord, elle aurait probablement été plus réussie s'il n'y avait pas eu de nuages... (cliquez là pour en avoir une plus grande...)

Vous remarquerez aisément que toutes les étoiles n'ont pas du tout la même modification d'aspect en passant d'une image à l'autre. Ce n'est pas étonnant, toutes les étoiles n'ont pas la même couleur. Si vos images sont numériques, évitez de leur faire subir toutes sortes de traitements exotiques afin de "les améliorer"...

Maintenant, il nous faut passer à la grosse étape: le traitement des données. Le but va être de placer les étoiles des images sur un diagramme traçant leur magnitude dans le vert (m_v) en fonction de leur différence de magnitude dans les deux couleurs utilisées (m_b - m_v). Ce graphique s'appelle un diagramme B-V chez les "pros"...

A partir d'une image argentique, il est possible de projeter les négatif sur un écran et de mesurer les diamètres des étoiles. Plus elles sont "grosses" et plus leur magnitude est faible. Il suffira alors de connaître les magnitudes réelles de deux étoiles du champ pour étalonner toutes nos mesures.

A partir d'une image numérique, c'est plus facile. Il existe des logiciels permettant de faire les mesures à l'écran soit des diamètres d'étoiles soit des largeurs à mi-hauteur (FWHM en anglais) ou encore qui intègrent sur toute la surface de l'étoile. Cela peut être IRIS par exemple logiciel très complet de traitement d'images astronomiques, ou B-V, sans prétention, mais réalisé par Robert pour mener à bien ce traitement. Les deux sont gratuits.

	Les références choisies ici étaient les étoiles 1 et 2 indiquées sur l'image ci-contre:
	Pour la 1, mv = 7,36 et mb - mv= 0,1
	Pour la 2, mv = 5,46 et mb - mv= -0,04

Pour étalonner les magnitudes, voici un exemple:

Le but est d'avoir les véritables magnitudes de chaque étoile à partir de la mesure de diamètre ou de surface faite sur les images. on suppose que (mv réel) = a x (log v) + b, et que (mb - mv) réel = a' x (log b - log v) + b' Il suffit alors de calculer a, b, a' et b' pour obtenir toutes les magnitudes "réelles". (Vous pourrez vérifier qu'avec les valeurs indiquées plus haut, a = -10.78, b = 13, a' = -1.22, et b' = 0.61). Bien entendu, placer toutes ces mesures dans un tableur paraît une bonne idée.

A ce stade, on se retrouve avec un tableau de nombres pas très drôle. Mais si l'on trace mv en fonction de (mb - mv), on obtient quelque chose de tout à fait étonnant:

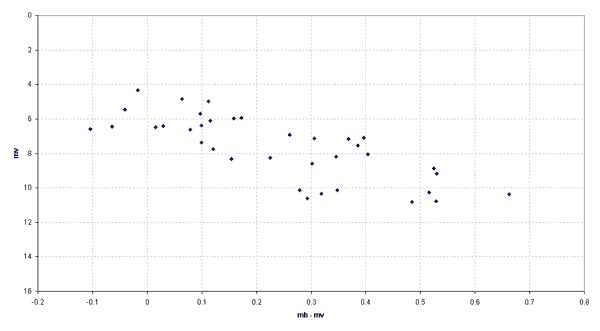Vous voyez? Les étoiles ne se répartissent pas du tout au hasard, mais selon une bande assez régulière. Plus l'étoile est à gauche et plus elle est bleu, plus elle est haute, et plus elle est brillante. Cette bande s'appelle la séquence principale, et on sait maintenant que c'est là qu'une étoile passe la majeure partie de sa vie, pendant qu'elle transforme son hydrogène en hélium, comme le fait notre Soleil.

Bien, on tient quelque chose de rigolo... Mais quel rapport avec la distance de notre amas? Et bien, on peut déjà se dire que si on l'éloigne de nous, les couleurs des étoiles ne changeront pas (axe horizontal), mais que les étoiles sembleront, vues d'ici, moins brillantes, leur magnitude va augmenter, la courbe précédente va donc se décaler vers le bas, d'autant plus que l'amas sera éloigné. On tient donc notre tremplin vers la distance. Sauf qu'encore une fois, il nous faut une référence: un diagramme étalon qui serait obtenu avec des étoiles dont on connait les distances, ou pour lequel les étoiles seraient, par calcul, placées toutes à la même distance...

Comme on peut mesurer les distances des étoiles les plus proches par parallaxe, un tel graphique peut être construit. Il s'appelle le diagramme Hertzprung-Russel (ou H-R pour les intimes). Voici celui qui a été construit grâce aux étoiles dont le satellite HIPPARCOS a pu déterminer les distances:

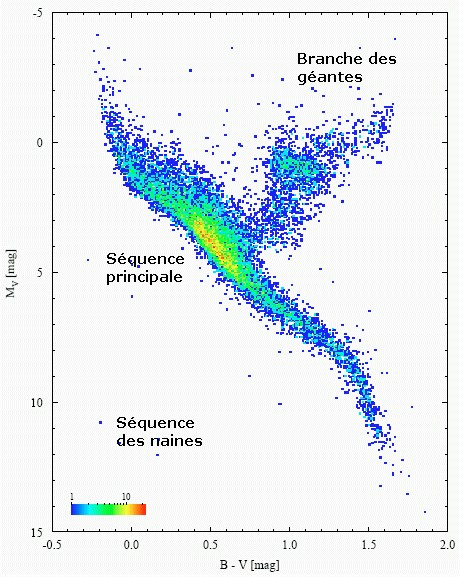
	Vous avez vu? Il n'y a pas que la séquence principale sur ce diagramme, mais aussi la branche des géantes. L'amas des pléiades est encore trop jeune pour en contenir... Tiens, on doit donc pouvoir se servir d'un tel graphique pour trouver l'âge d'un amas?... Ce sera pour une prochaine fois...
	En fait, la "seule" différence entre ce diagramme et le notre, est l'axe vertical, qui porte cette fois la "magnitude absolue": c'est celle qu'aurait l'étoile si elle était à 10 parsecs de nous, ou 32,6 années lumières...

Il n'y a plus qu'à placer "notre" courbe sur ce diagramme étalon, et à évaluer la différence:

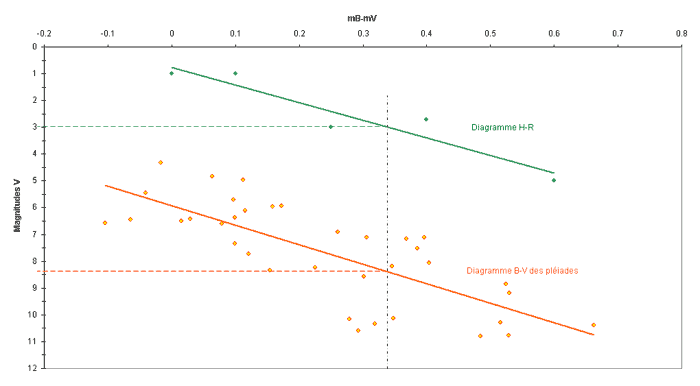En vert, quelques points centrés sur la séquence principale étalon, en orange, le diagramme B-V des pléiades. Les deux courbes sont bien sensiblement parallèles. D'un coup d'oeil distrait, les étoiles des Pléiades sont moins brillantes que celles qui constituent le diagramme HR, celles-ci sont à 32,6 A.L. Les Pléiades sont donc plus loin, mais où?...

Notre sauveur final est la règle de Pogson, bien connue des astrophysiciens:

Ici, le décalge des deux courbes (m - M) vaut environ 5,5, ce qui donne d # 126 pc # 410 AL

Vous vous rendez compte? On vient de déterminer la distance des Pléiades à partir de deux images à basse résolution prises dans de mauvaises conditions!... Je suis d'accord, de meilleure qualité, elles auraient donné peut-être d'autres valeurs? Quoiqu'il en soit, la valeur couramment admise actuellement tourne autour de 430 à 450 AL. Ce qui donne d'abord 7% d'écart, et ensuite envie de recommencer sur d'autres amas. Et peut-être y verra-t-on apparaître cette fameuse branche des géantes?...