Comment mesurer la distance de Neptune, et sa masse en deux photos?...

Neptune est ce qui se fait de plus lointain comme planète, dans notre système solaire (Pluton ayant la malchance de s'être fait déclassée...). Le défi est cette fois de mesurer sa distance au Soleil, et obtenir sa masse, en seulement deux images. Mais pas n'importe lesquelles...

Ies données nécessaires doivent être obtenues grâce à 2 images prises à environ une journée d'intervalle, montrant le déplacement apparent de Neptune par rapport aux étoiles (pour obtenir la distance Soleil-Neptune), et le mouvement de Triton, son satellite (pour avoir la masse de la planète).

Attention: afin de respecter les approximations réalisées dans les calculs, les images doivent être obtenues le plus près possible de l'opposition (Soleil, Terre, Neptune presque alignés).

Voici le document:

Certes, il y a 3 images... Mais 2 suffisent. Triton est le petit point tournant autour de Neptune. La flèche indique un autre satellite de Neptune (Néréide) dont il ne sera pas question ici.

Pourquoi Neptune se déplace t-elle par rapport aux étoiles? Parce qu'elle tourne autour du Soleil, mais surtout parce que nous aussi, sur Terre orbitons autour de notre étoile. Lors de l'opposition, la Terre double Neptune.

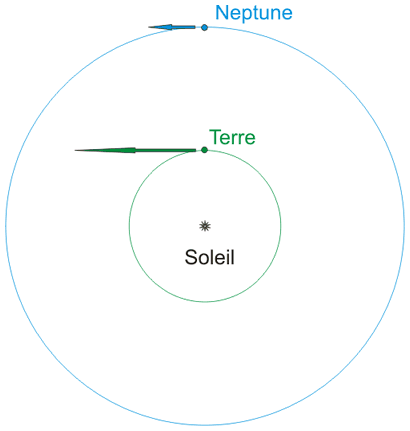	La Terre est en train de doubler Neptune sur son orbite, lors de l'opposition. Le schéma n'est pas à l'échelle.
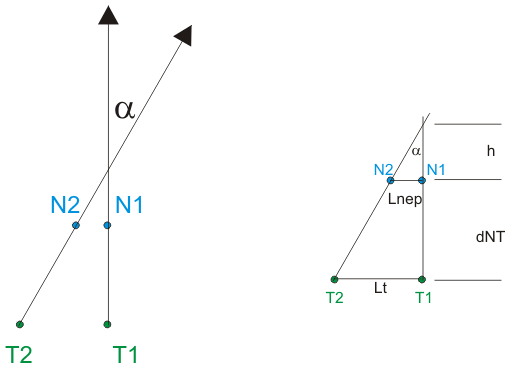	-Entre deux dates, Neptune (N) et la Terre (T) se sont déplacées, quasiment sur des droites si l'intervalle de temps entre deux observations est bref (quelques jours). Supposons ici que les déplacements indiqués sont réalisés en 1 seconde...

Dans le dernier croquis, si une seconde sépare les positions des deux planètes, alors les deux distances Lnep et Lt correspondent aux vitesses des deux astres en m/s.

On obtient: alpha = Lnep / h = Lt / (dNT + h) ou alpha = Vnep / h = Vt / (dNT + h), où alpha (très petit) est alors en radians parcourus en 1s. Les photos nous permettent d'évaluer le déplacement angulaire de Neptune en quelques heures, ramené à une seconde, ce sera le "alpha" de notre formule.

Dans la formule précédente, on ne connaît pas "h", ni "Vnep". Par contre Vt = 30 000 m en 1s, Vnep = racine carré (G.Msoleil / rnep) et dNT = rnep - rt. Bien sûr rnep et rt sont les rayons des orbites des deux planètes (supposées circulaires), G est la constante de gravitation: G = 6,67.10^-11 S.I, et Msoleil = 2.10^30kg

Un peu d'algèbre pour éliminer h, et n'avoir plus qu'une seule équation:

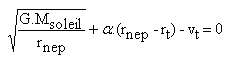-La seule inconnue de l'équation est alors rnep, le rayon de l'orbite Neptunienne, alpha est votre mesure expérimentale, les autres valeurs sont des données obtenues par ailleurs...

Si vous le sentez, vous pouvez toujours tenter de résoudre cette équation... Personnellement, je n'essaie même pas...

Un moyen très simple est d'utiliser un tableur, d'entrer une liste de valeurs incrémentées pour rnep, de placer toutes les autres valeurs en références absolues, et de tracer la fonction indiquée ci-dessus dans l'encadré. Là où la courbe passera par zéro, vous aurez le bon rayon de l'orbite de Neptune... Si vous êtes vraiment trop épuisés, voici une page utilisable sous Excel©. Cela donne la courbe ci-dessous:

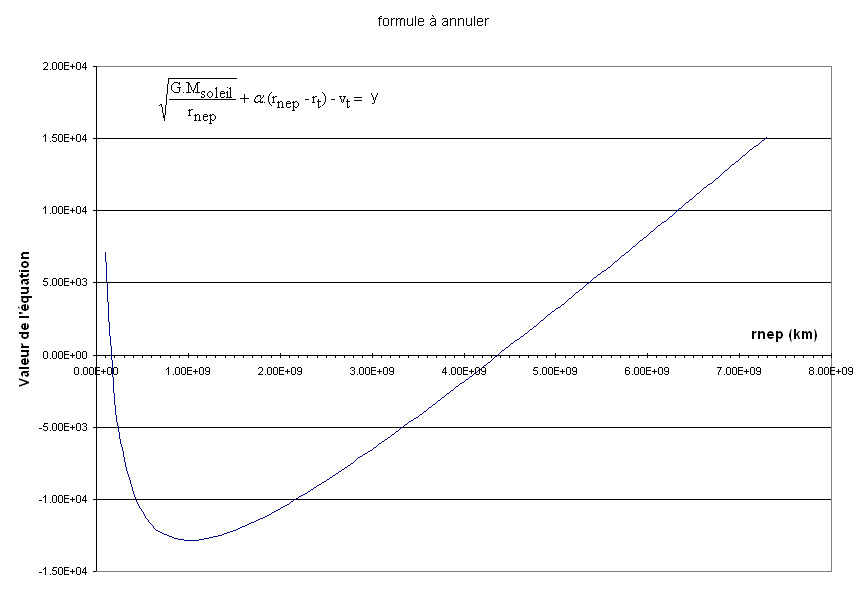
Cette courbe a été obtenue grâce aux mesures faites sur l'image d'introduction: en 23h, Neptune a bougé de 43 pixels, comme il y a à cette échelle 27 pixels pour 1 min d'arc, cela revient finalement à alpha = 5,6.10^-9 rad parcourus en 1 seconde par Neptune sur le fond de ciel.

La courbe s'annule deux fois, la première valeur étant une valeur aberrante. La seconde indique 4,4 milliards de kilomètres, au lieu de 4,5 milliards de km réels. De l'ordre de 2% d'erreur. Honnête non?

Et pour peser Neptune? Il faut cette fois utiliser son satellite et mesurer sa période orbitale. Puis, comme on connait maintenant notre distance à Neptune, on détermine le rayon de l'orbite de Triton. Enfin, l'application de la 3ème "loi" de Képler donnera la masse de Neptune. Voyons ça:

48h30 (T) séparent ces deux images. Agréablement pour nous, le plan orbital de Triton est vu quasiment de face... Un angled'environ 138° a été parcouru. D'après l'échelle, Triton est à 16 seconde d'arc de Neptune (beta)

Le rayon orbital de Triton vaut donc: r = d(terre-nep).tan beta = 330 700 km (En réalité: 355 000 km)

Képler nous dit que:

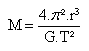Le calcul final donne: M Neptune = 1,04.10^26 kg (au lieu de 1,02.10^26 kg)...

Juste avec deux images, obtenir la distance et la masse d'une planète aussi lointaine, je ne sais pas pour vous, mais Robert en est tout estourbi...