Comment mesurer le rayon de la Terre, avec les caméras FRIPON?

       Encore une mesure du rayon de la Terre?... Oui, certes, on connaît la méthode classique d'Eratosthène, les Fans de Robert connaissent sûrement la méthode du "manche à balais", en voici une toute neuve qui utilise le réseau de caméras FRIPON...

Comme je sens tout un tas de questions qui surgissent, tentons de répondre à certaines:

Qu'est-ce que le réseau FRIPON? C'est ici. Le sigle est formé à partir de "Fireball Recovery and InterPlanetary Observation Network" Pour résumer, c'est un réseau de caméras "Fish eye", donc à 180° de champ, qui pointent vers le zénith, et dont le but est de surveiller le ciel afin de capturer les images de bolides et autres lumineuses étoiles filantes, afin de pouvoir retracer les trajectoires de ces blocs de roches ou cailloux plus modestes qui arpentent le système solaire, ou bien de retrouver la météorite au sol en comparant les trajectoires enregistrées par plusieurs caméras. Les images sont prises à intervalles de temps réguliers, de jour comme de nuit.

La carte du réseau de caméras est disponible sur le site de FRIPON ci-dessus, ou bien ici, si l'adresse n'est pas changée à notre insue...

Nous connaissons les outils, mais quel est le principe de la manip? c'est simple, comme pour l'expérience d'Eratosthène, le Soleil est, à midi solaire, à des hauteurs différentes dans le ciel pour des observateurs situés à des emplacements différents sur le même méridien.

Vous avez repéré les mots clefs? "midi solaire" et sur le "même méridien"

Il suffit donc de partir à la chasse aux images répondant à ces deux critères, sur la carte de FRIPON. Ah... il faut aussi qu'il fasse beau, et que le Soleil soit visible sur l'image.

Ca doit aussi pouvoir se faire sur des étoiles brillantes identiques, plein sud au même moment sur deux images prises de lieux différents.

Je vous rappelle que le but de Robert n'est pas de faire dans la haute précision, mais de donner des pistes de lignes de conduites que vous pourrez améliorer à loisir.

Voici un couple d'images servant d'exemple:

Depuis Carcassonne	Depuis Capelle la Grande, près de Dunkerque

Ces images n'ont pas été choisies au mieux: Le Soleil n'est pas tout à fait au méridien, les heures ne sont pas exactement les mêmes. Mais ça vous donnera une idée.

Les mesures sont simples: il nous faut la hauteur du Soleil au-dessus de l'horizon pour ces deux lieux. Avec un logiciel de graphisme quelconque, il suffit de mesurer "h" et "L" en pixels, ou en millimètres sur un écran, ou sur du papier si vraiment les bugets sont en baisse.

Comme "L" correspond à 180°, un simple "produit en croix" vous permettra de trouver "h" en degrés au-dessus de l'horizon.

Par exemple, avec ces deux images, j'ai trouvé environ h1 = 49,3° depuis Carcassonne, et h2 = 41,8° depuis Dunkerque. Le Soleil est donc bien plus haut dans le ciel depuis le Sud de la France que depuis le Nord, ça nous rassure sur la rotondité de la Terre...

Mais comment utiliser ces angles pour retrouver le rayon de la Terre? Voici un schéma un peu plus technique:

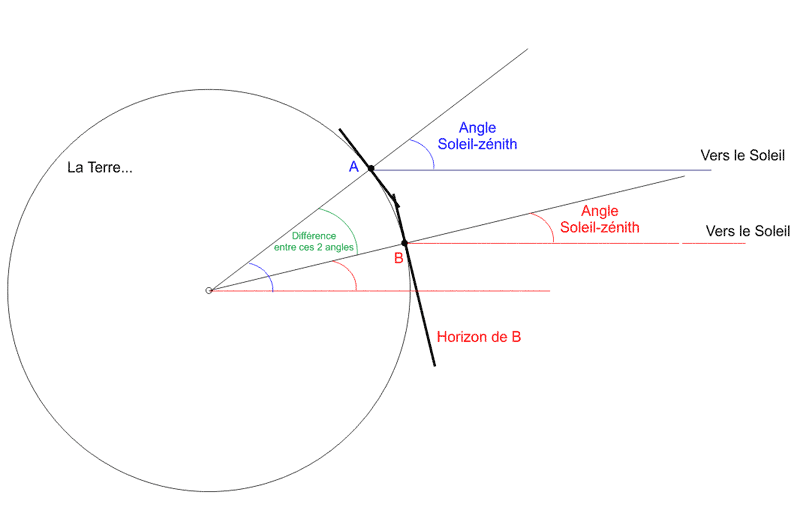
Depuis les deux villes A et B, le Soleil n'a pas le même écart angulaire avec le zénith. La différence entre ces deux angles est identique à l'angle entre les deux villes depuis le centre de la Terre.

Vous pouvez remplacer dans la phrase précédente "zénith" par "horizon", et la relation reste la même.

Ainsi, h1 - h2 = 49,3 - 41,8 # 7,5°, c'est aussi l'angle entre A et B depuis le centre terrestre.

Ah, il nous faut aussi la distance entre les deux villes: Géoportail rend bien service ici, et nous annonce 886 km.

Dernier petit produit en croix avec cette correspondance:

886 km pour 7,5°

Périmètre pour 360°

Et on trouve un périmètre terrestre de 42500 km, au lieu des 40000 km connus actuellement, soit 6% d'écart relatif... Acceptable vue la haute méticulosité des manipulations...

Bien sûr, si vous voulez le rayon terrestre, il suffit de diviser la circonférence par 2.pi, ce qui donne environ 6800 km au lieu de 6400 km

Si avec tout ça vous pensez encore que la Terre est plate...